Delta Values
Traders can take advantage of the key to estimating that an option will expire in-the-money
New traders often think they’re drowning in information when they open their first options chain. Dealing with puts and calls, dozens of strike prices and numerous expiration dates can feel like shopping for a jar of spaghetti sauce in a supermarket aisle jammed with simply too many choices. But after learning the basics of options mechanics, traders should consider a critical column in the options chain: delta.
Every options contract has a delta value. In mathematical terms, an option’s delta is the rate of change in an option’s price with respect to the stock price. Another interpretation, perhaps more pertinent to traders, is that an option’s delta is the approximate probability of that option expiring in-the-money. To see this in practice, pull up an options chain on a favorite stock.
Notice that the at-the-money (ATM) options—those with a strike price roughly equivalent to the underlying’s current trading price —have a delta of around +/- 0.50. In-the-money (ITM) options, those with intrinsic value, have a delta closer to +/- 1.00; and out-of-the-money (OTM) options have deltas closer to 0.
Reframed as probabilities, options with a delta near +/- 1.00 have a near 100% probability of expiring ITM, while those with a delta of +/- 0.50 have a 50% probability of expiring ITM, and so on.
Traders can use that information to decide which strike price they want to trade. Because an option’s price is based on the market’s expectation of movement—and the delta is, too—traders may buy or sell around certain expectation levels with the belief that markets are overstating or understating expectations of future movement.
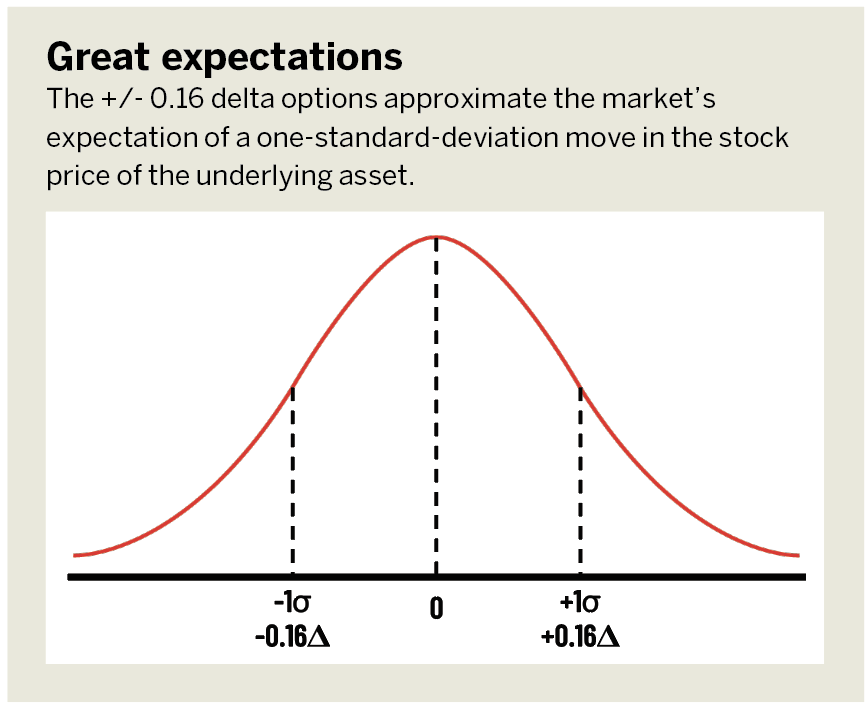
For example, many traders play around +/- 0.16 delta options that represent the market’s expectation of a one-standard-deviation move. By selling the 0.16 delta call and -0.16 put, a trader has created a short strangle that makes money if the underlying moves less than the market’s expectation of that stock’s one-standard-deviation move.
Look at the options chain for Apple (AAPL) with options expiring in December. Now, locate the 0.16 delta call and -0.16 delta put. Given those delta values, the market is expecting a roughly 68% probability for Apple to stay within those call and put strike prices by expiration. Put another way, if 100 simulations were run from now until December expiration, the market is expecting Apple to stay within those two levels in about 68 of those 100 simulated paths.
Note, however, that delta values aren’t static and are likely to change based on any change in inputs to the option’s price, including time to expiration, interest rates, underlying price and expectation of movement. Just as stock prices update on a microsecond level, delta values do so, too. When trading probabilities, it’s best to manage actively and stay small.
Michael Gough enjoys retail trading and writing code. He works in business and product development at the Small Exchange, building index-based futures and professional partnerships.