Gambling vs. Stock Options
Don’t buy into the hype—understand the probabilities behind options

Who makes more money in Las Vegas—the gambler or the casino? OK, a gambler might win once in a while and thus believe it can happen again and again. But over time, the casino builds wealth while the gambler’s wastes away. Given the choice, wouldn’t it make more sense to be the casino than the gambler? Luckily, exchange-traded options give investors a legal way to play the role of the casino without the capital that buying a casino requires.
Every trade has a winner and a loser. When it comes to options, the sellers (analogous to the casino) tend to win over time, making small prof- its consistently. Option buyers (the gambler) tend to lose but occasion- ally land a big winner.
Sure, selling options has been profitable, on average, for the past 14 years, But don’t fall for those ads that say, “Make 800% in 15 minutes with this simple strategy!” They’re a gamble.
Investors can use options not only for consistent premium selling but also to take a shot on a hunch once in a while, assuming of course, that the investor knows the risk and odds before entering the trade.
Suppose one buys the 291-strike call in SPY (the S&P 500 ETF) expiring in seven days for $0.07 per contract. This trade packs huge potential! If SPY (trading at $285.50 as of April 2, 2019) moves more than $7 dollars in the next seven days, an investor would make $100 for every additional dollar SPY moves higher.
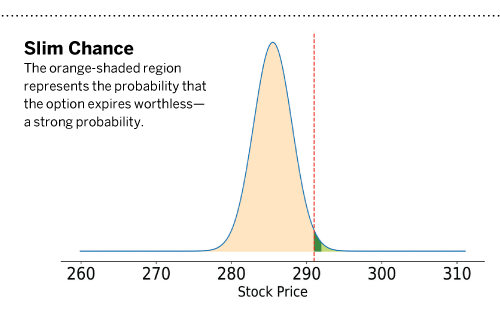
Say that SPY closes at $292 or higher by expiration. The $0.07 option is now worth at least $1, for a 1,300% increase! But, what are the odds? According to theoretical probabilities, that has roughly a 0.78% chance of occurring. What about the probability that the option will be worth at least $0.01 by expiration? Theoretically, that has a 2.15% chance of occurring. The other 97.85% of the time an investor is expected to lose the premium invested.
1,300% increase! But, what are the odds? According to theoretical probabilities, that has roughly a 0.78% chance of occurring. What about the probability that the option will be worth at least $0.01 by expiration? Theoretically, that has a 2.15% chance of occurring. The other 97.85% of the time an investor is expected to lose the premium invested.
“Slim chance,” shows the possible distribution of stock prices by the expiration date of the option. The orange shaded region represents the probability that the option expires worthless. The green area to the right of the red dashed line represents the likelihood that the option expires in the money. The light green area represents the likelihood that that option is worth at least $1 by expiration, yielding a return of 1,300%. Orange probability = 97.85%, dark green probability = 2.15%. Light green probability = 0.78%. Investors who buy options are betting on the little green area. If they sell options, they’re betting on that orange area.
Now to the historical backtest. “The price is right,” is showing summary statistics for the long call since 2010, which indicates it has had roughly the same probabilities and duration as the one trade in the example:
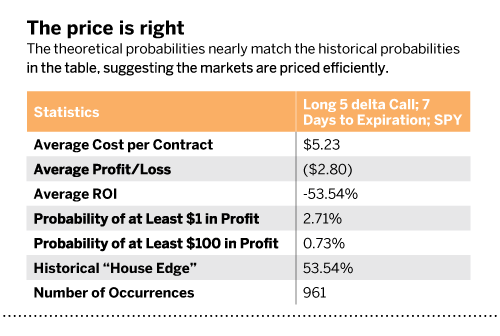
Key points to take away from this table include the fact that the theoretical probabilities listed above the table nearly equal the realized historical probabilities in the table. That suggests the markets are priced efficiently, and traders can use statistical models to estimate probability of profit with decent accuracy.
Second, the “house edge” is the same as the ROI. Those familiar with casinos and gambling realize casinos use this 54% house edge to determine the payback percentages, or ROI, to players. The house edge for most casino games ranges between 1% and 10%, meaning that for every bet gamblers place in the casino, they can expect to lose between 1% and 10% of total bets over the long run.
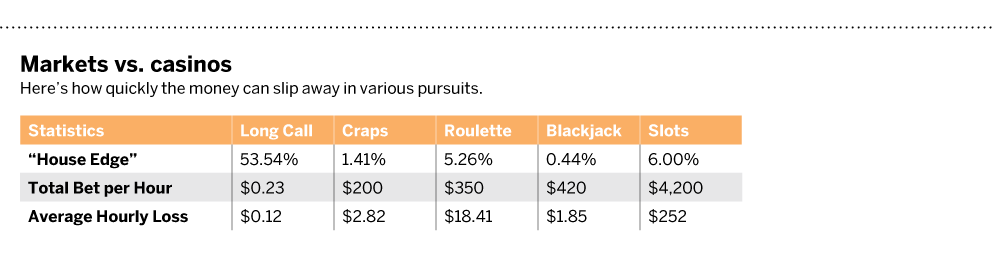
It may seem like a casino game like roulette with a house edge of 5.26% represents a better bet than the long premium example above with a house edge of 54%. However, consider this: in roulette, a player may have 50 spins per hour, compared to this long premium trade where an investor buys one contract every 30 hours (roughly five business days).
Gamblers tend to lose more in a casino than investors lose by buying options
Assume a gambler bets the same amount on roulette as the amount of premium an investor buys. In other words, $7. That translates to a notional value of $350 per hour in bets in roulette versus $0.23 per hour in bets for the long call. Multiply those figures by their respective house edges and one can expect to lose roughly $18.41 per hour in roulette versus only $0.12 per hour on the call. So investors can “play” for longer with the long call because they lose money more slowly than in a casino game, even though the house edge on the call is astronomically higher.
Below are comparisons of the long call and various casino games wagering $7 per bet.
Takeaways—the far out-of-the-money long call strategy
- Expect to profit at least $1 around 2.15% of the time.
- Expect to lose 54% of the total premium invested over the long run.
- Markets are efficient because the theoretical probabilities of profit match the realized probability of profit.
- Casinos give players better odds per bet, but players lose more at a casino by placing many more bets per hour there compared with buying a call every week.
- Casinos are analogous to option sellers. Gamblers are analogous to option buyers.
Anton Kulikov is a trader, data scientist and research analyst at tastytrade.





















