Counting Outs & Calculating Pot Odds
A WSOP poker pro teaches the math you need to succeed

Savvy poker players can forecast the probability that they hold the best hand in the game. Here’s how you do it.
Calculating pot odds
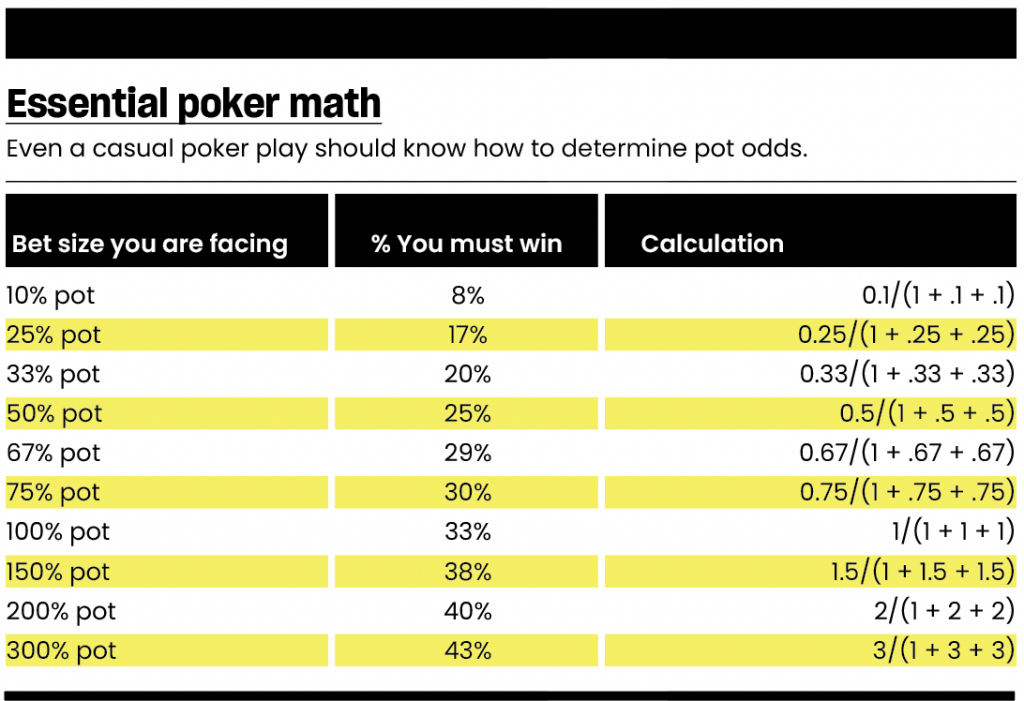
Pot odds determine how often you need to win a pot to break even. It’s based on the bet you’re facing in relation to the size of the pot. Here’s the equation: % Required to win = bet/(pot + bet + bet). It can determine how often you need to win to continue anytime you’re facing a bet when against one opponent.
Suppose your opponent bets $100 into a $100 (100%) pot. In this situation, you have to call $100 to win $300 total (the $100 pot, your opponent’s $100 bet and the $100 you are putting in). That means you need to win the pot 33% of the time or more to profit 100/(100 + 100 + 100). See Essential Poker Math, below.
If you know it will win more than 33% of the time based on your hand’s strength or the likelihood your hand improves to the best hand (which will be discussed soon), then you should call and continue in the pot. If it wins less than 33% of the time, you should consider folding.
The chart below lists bet sizes you may face and the percentage of the time you must win to continue profitably.
You may be surprised that no matter how much your opponent bets, the most you will ever need to win is only 50% of the time to break even. That said, you will find almost no one in the real world bluffs too often using a bet of three times the size of the pot.
Facing a bet with players yet to act behind you, consider how often you will be raised and thus forced to fold your hand. With players yet to act, you usually need to win far more than your pot odds dictate to continue.
Counting outs
When you have a draw (a hand that’s almost certainly behind at the moment but could improve to the best hand if the next card is a specific required card), you must figure out how many outs you have to improve.
• For a gutshot straight draw (6-5 on a 9-8-2 flop), you have four outs (four 7s).
• With two overcards (K-Q on 8-7-2), you have six outs (three Ks and three Qs).
• With an open-ended straight draw (7-6 on 8-5-2), you have eight outs (four 10s and four 5s).
• With a flush draw (two cards of the same suit in your hand and two cards of that same suit on the flop), you have nine outs (the remaining nine cards of the same suit).
• With a flush draw and a gutshot straight draw, you have 12 outs (notice one of the straight cards also makes a flush).
Note that all of your outs may not actually improve your hand enough to make it the best. When you have two overcards, such as J-10 on 7-6-2, if the turn is a 10, you could be drawing dead if your opponent has 9-8 or way behind if they have 7-7, 6-6, 10-7, 7-6 or Q-Q.
If you have a low flush draw, such as 4↔-3↔ on Q↔-J♥-6↔, if the turn is a spade giving you a flush, you could lose to numerous better (higher high card) flushes. For this reason, draws to the best possible hand are always much better than draws to strong but potentially second-best hands.
As a shortcut to determine roughly how often your draw will complete, take the number of outs you have, multiply it by two and make it a percentage. That will let you know how
often your draw will complete on the next card.
For example, if you have an eight out open-ended straight draw, it will arrive on the next card roughly 8 x 2 = 16% of the time. If you have a 15 out straight flush draw, it will arrive 15 x 2 = 30% of the time.
If there are two cards to come, assuming you will see them both (which may or may not be the case), you can multiply your number of outs by four and make it a percentage.
If you have an eight out open-ended straight draw, for example, it will arrive on the next card roughly 8 x 4 = 32% of the time. If you have a 15 out straight flush draw, it will arrive 15 x 4 = 60% of the time.
Not that simple
Poker math is complex because players have so many things to consider, even in somewhat simple situations. If you have an open-ended straight draw with 7-6 on 8-5-2, consider what happens if the turn is a 6 or 7, giving you a pair.
If your opponent bets again, you certainly can’t fold because of having more outs when you are behind and potentially even being ahead.
Another likely possibility is you could check/call your opponent’s flop, the turn checks through and you fail to improve by the river. You may then have a profitable bluffing opportunity. Alternatively, you may hit your draw on the turn, check/call a bet, and then have a check/raise all-in on the river get called, winning your opponent’s stack.
Yes, poker requires thought. But if you break it down to its basic building blocks, you can begin developing reasonably sound strategies. If you consistently consider the basic math in this article, you’ll be well on your way to success.
Jonathan Little, a professional poker player and WPT Player of the Year, has amassed more than $7 million in live tournament winnings, written 14 best-selling books and teaches at pokercoaching.com. @jonathanlittle















