Butterfly Spreads
The good news is that investors can slightly tweak many option strategies, including the butterfly, to gain maximum control over the risk and reward.
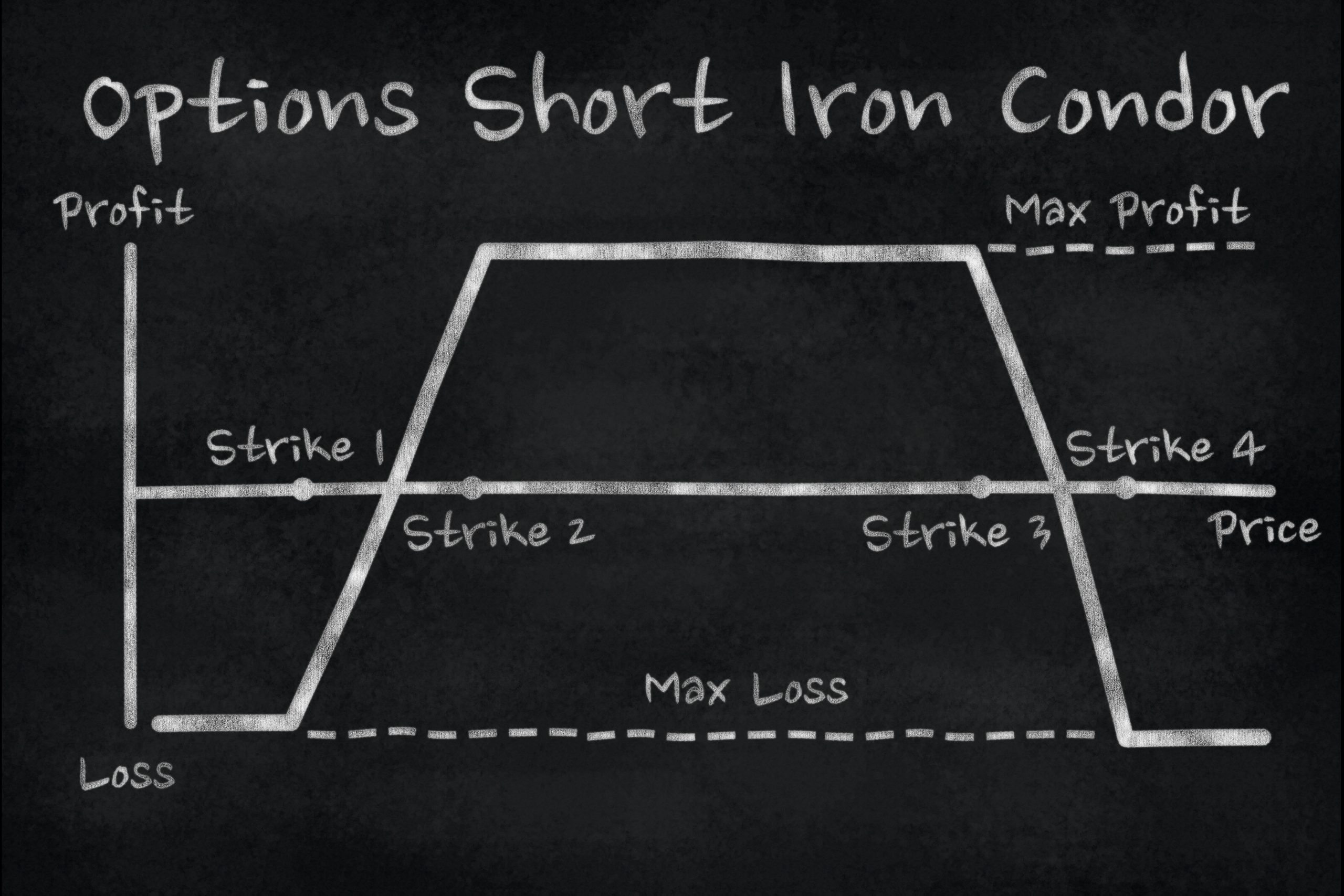
The butterfly option strategy owes its popularity to its high reward-to-risk ratio, which might range from 4 to 1 to even 10 to 1. That’s risking $1 to make $4. The relatively low risk and high profit potential for the butterfly make it tempting. Who wouldn’t want to make $400 while only risking $100? The drawback is that low risk/high reward strategies generally have low probabilities of success. (See “Low, high,” below.)

Take for example the butterfly trade, a trade with a low probability of success but a high theoretical return on investment. Perhaps an investor has a hunch that Schlumberger (SLB) will be at 35 by the end of the next expiration. As of mid-August, the 32.5/35/37.5 Schlumberger butterfly in October had a $50 cost and a $200 maximum profit potential. In other words, it risks $50 for a profit potential of $200. (See “Trading the butterfly,” below.) But the theoretical probability of success on the trade is slightly under 30%. Not so great.
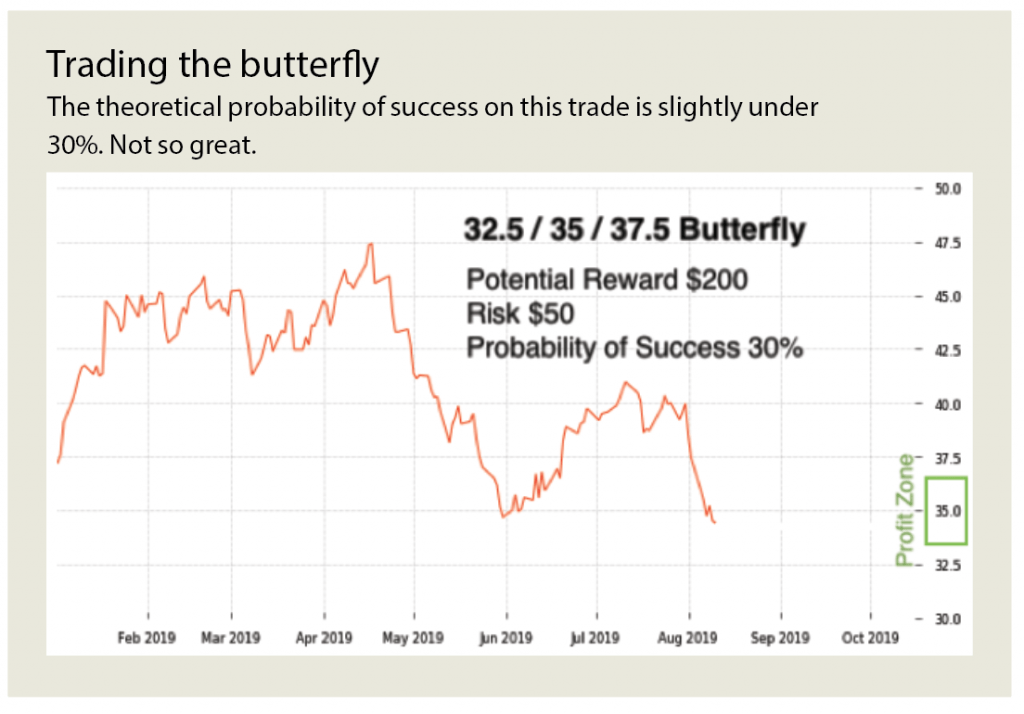
This trade has such a low probability of success because the butterfly requires that the stock remain in a relatively narrow range between its break even points, or even “pin” the short middle strike at expiration to reach its max profit. The stock has to be between $33 and $37 to make even a penny of profit; it would need to land at $35 exactly for maximum profit.
Investors can slightly tweak many option strategies, including the butterfly, to gain maximum control over the risk and reward and therefore the probability of success. Depending upon the objective, one trade might be ideal for the particular circumstance.
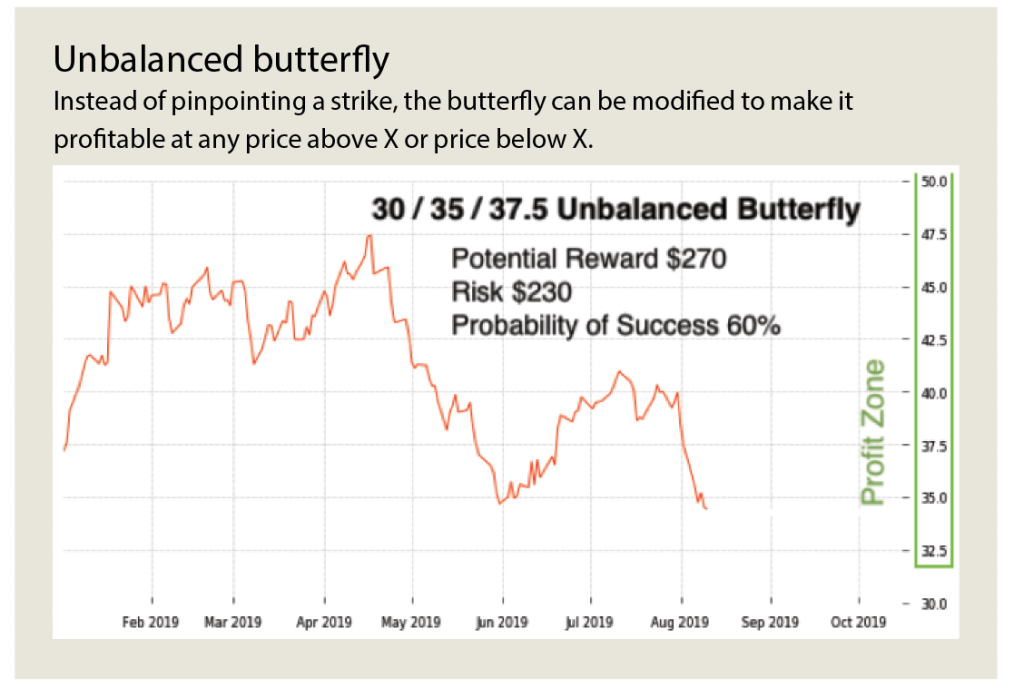
For the butterfly to have a considerably higher probability of success, investors can unbalance it. (See the Advanced article in this series.) That makes the “profit zone” much higher. Instead of pinpointing a strike, the butterfly can be modified to make it profitable at “any price above X or price below X.” Going back to the Schlumberger example, the strikes can be modified to create the 30/35/37.5 unbalanced butterfly with considerably greater risk (in the example below it is $230) but with a considerably greater probability of success—roughly 60%. Here, instead of a relatively small “profit zone” and a 4-to-1 reward-to-risk ratio, the “profit zone” is much wider, and the reward-to-risk is a more modest 1-to-1.
Which is better: “regular” butterfly or unbalanced? In practice, neither. It’s all about using either to find one’s preferred balance between risk, reward and probability of success.
Click here to read the second part of this series.
Michael Rechenthin, Ph.D., (aka “Dr. Data”) is head of research and data science at tastytrade.