Probability Matters
Get serious about investing by attaching a numerical probability to every trade
It’s fun to speculate about cultural, political or economic events that might happen in 2023. But when it comes to investing, it’s preferable to keep entertaining guesses out and quantifiable outcomes in.
That means attaching a probability number—between 0% and 100%—to where a stock price might be at some point in the future.
When an investor knows the probability that a stock that’s now $100 might drop to $95 in the next 45 days, that can be the basis of a potentially successful trading strategy.
That probability number is heavily dependent upon an estimate of the volatility of the stock. A lower volatility means larger percent price changes are less probable, and a higher volatility means larger percent price changes are more probable.
But volatility is a snapshot. It captures the market’s opinions right now about what the stock might do in the future. Factors that could cause a stock to have larger or smaller price changes are compressed into volatility by market activity. Examples include earnings, product releases, government decisions and the economic climate. When those factors change, volatility can change, too.
So, what happens when an investor makes a probability-based decision when the stock has 20% volatility, and then the stock’s volatility moves to 30% the following week?
Well, the probabilities change. But why, and by how much?
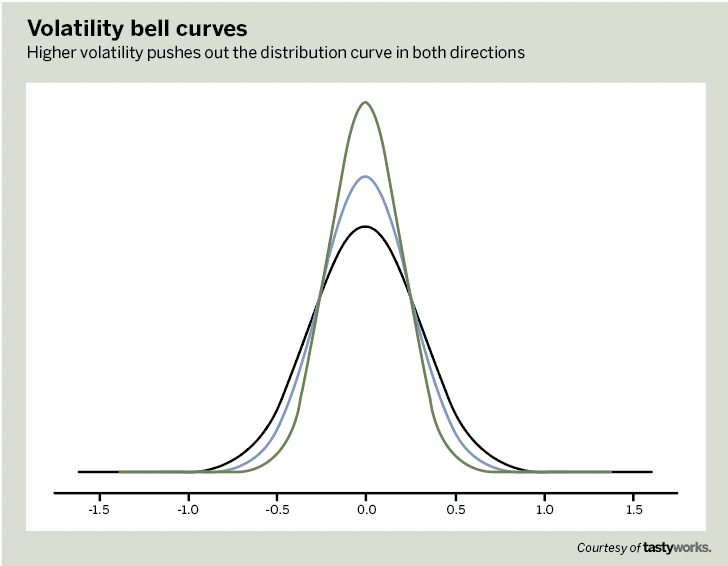
Volatility affects probability via the normal distribution curve, and that curve gives us the probability that a stock will reach a particular higher or lower price.
Consider three normal distribution curves (in the chart above), each based on a different volatility: 20% (green), 25% (blue) and 30% (black). The height of the line indicates the probability.
The shape of the curve doesn’t change much, with the highest probability that the stock will stay close to its current price no matter what the volatility. But higher volatility pushes the sides of the normal curve higher, which means there’s a somewhat higher probability that the stock will reach a higher or lower price when volatility is higher.
But if a trader makes a decision based on probability—particularly a short options strategy, like a bullish short put based on current volatility—the volatility changes and changes the probability. Was the trader’s original decision wrong? Or how does the trader adjust?
Consider a short put with a 95 strike price on a $100 stock. It’s a bullish strategy, typically with a better than 50% probability of making a profit. Assume the investor shorts the put when volatility is 20%, then one week later volatility is 30% and the stock is still $100. These are the probabilities that the 95 put will expire worthless (POE, probability of expiration) at different times to expiration (DTE).
•
90 DTE / 20% vol ––> 83 DTE / 30% vol
69% POE ––> 62% POE
•
50 DTE / 20% vol ––> 43 DTE / 30% vol
74% POE ––> 68% POE
•
20 DTE / 20% vol ––> 13 DTE / 30% vol
86% POE ––> 81% POE
This shows that no matter how many DTE the option has when the trade is put on, as time passes and volatility rises, the probability that the option will expire worthless drops. But it drops more when there are more days to expiration. The probability of the put with 90 DTE dropped more than the put with 20 DTE.
As time passes, a change in volatility has a smaller impact. If that happens, the investor has to decide whether the probability is still high enough after the rise in volatility to continue to hold the position. If not, the trade could be closed or rolled to another put at a different strike and/or expiration that has a higher probability of profit.
It also shows the POE for options between 40 and 60 DTE start to be affected less than farther-dated options. Short options in that time frame begin to have growing positive theta (time decay), while still having enough premium to generate a higher return on capital.
So, if an investor is worried that a change in volatility will turn a high-probability trade into a low-probability trade, yes, it’s possible but would require volatility to triple or quadruple, accompanied by an adverse change in the stock price.
But most of the time, volatility won’t rise enough to make a big difference. That’s why an investor should trust the probability when making a trade and not worry about how a change in volatility would affect it.
Tom Preston, Luckbox contributing editor, is the purveyor of all things probability-based and the poster boy for a standard normal deviate. @thetompreston