Here’s the case for basing art and architecture on numbers from the Fibonacci sequence—and the case against it

The golden ratio has been capturing the imagination of scholars for more than 2,000 years.

Countless mathematicians, physicists, botanists, chemists and psychologists have pondered its meaning. Painters, sculptors, architects, composers and poets have embraced it for the structure it can provide.

There’s little doubt that it appears in the principles of geometry, the pattern of a sunflower’s seeds and the angles formed by the branches of a tree.

Some insist they see it reflected in the beguiling beauty of the Mona Lisa and embodied in the graceful architecture of structures as diverse as the Parthenon, the pyramids and the United Nations Secretariat Building. They profess to perceive its presence even in the dimensions of the human face and body.

True believers choose to understand it as the simple pattern that underlies the complexity of the universe. They’re in on the secret, and they see its almost magical qualities all around them. 

But is any of this really true? 

Discovering gold 

The golden ratio is related to the Fibonacci sequence of numbers, which begins with one and continues with the sum of the two preceding numbers. Thus, it starts with 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 and goes on to infinity.

Mathematicians in India knew about the sequence as early as 200 B.C., and Leonardo of Pisa, who was later called Fibonacci, introduced it to the West in the 13th century. Its relationship to investing was addressed in detail in the January/February issue of Luckbox. 

Then there’s that ratio. Two numbers are in the golden ratio if their sum divided by the larger number equals the ratio of the larger number divided by the smaller number. That comes out to about 1.618, and the decimal places continue forever without repeating. 

Now it happens that the ratios of Fibonacci numbers (2/1, 3/2, 5/3, and so on) approach the golden ratio. The higher the Fibonacci numbers, the closer they are to the golden ratio of 1.618.

And there’s more. Divide a line into two parts in such a way that the longer portion (a) divided by the smaller one (b) equals the sum of (a) + (b) divided by (a). Both then equal 1.618. 

The golden ratio yields the golden rectangle, which can be of any size so long as the ratio of the sides is 1.618. 

That’s all fine, but what does it mean?

Mixed results

The Fibonacci numbers and the golden ratio often appear in mathematics—in the geometry of pentagons, for example. They crop up in nature with surprising frequency—as in the number of petals in a flower. Meanwhile, there’s nothing to stop musicians or poets from basing rhythm on the Fibonacci numbers.

But what about using the golden ratio and golden rectangle as the basis for painting, sculpture and architecture? After all, this issue of Luckbox is devoted to art and design.

Promoters of the golden rectangle are convinced that people find its shape more pleasing than other rectangles. But psychological experiments demonstrate that people don’t exhibit a stronger preference for that configuration over others. Most test subjects just pick a random rectangle somewhere near the middle in dimensions, says Steven Strogatz, a professor of applied mathematics at Cornell University. 

He’s at a loss to explain why people proselytize for the golden rectangle. “It has some kind of appeal that I can’t explain,” he says. “It’s something psychological, and I think it’s related to Western culture. I don’t think they believe in this stuff in India or Japan.”

But adherents tend to see their golden ideal everywhere. Take the example of the Parthenon, the ancient Greek temple atop the Acropolis in Athens.

Those who promote the golden rectangle’s place in architecture are fond of superimposing the shape over photos or diagrams of the Parthenon. They hold that up as proof that the building was based on the golden rectangle.

Yet, nothing in the historical record indicates that Phidias, the artist who directed construction of the Parthenon, employed the golden rectangle on the job site.

What’s more, acolytes of the golden rectangle draw the shape over images of the Parthenon with such broad, heavy lines that they distort the contours of the building, forcing it to conform to the formula, says Keith Devlin, an emeritus mathematician at Stanford University who’s devoted three of his books to Fibonacci.

Actually measuring the building can prove even more damning to the notion that the golden rectangle or golden ratio dictated the dimensions. John Ronan, a Chicago architect who teaches at the Illinois Institute of Technology, points out two facts that he says contradict the golden theory.

First, the columns at the front of the Parthenon aren’t evenly spaced. In absolute defiance of the golden rectangle, the outer columns are closer together than the inner ones.

“Undoubtedly, they drew it up with all the spaces being equal and then found it just didn’t look right,” Ronan says. “So, they scooted in the end columns.”

Moving those columns toward the center would not have improved the structural strength of the building because the outer columns bear less load than the inner ones, he notes.

Second, the builders intentionally curved the columns. Bowing the bottom third outward—just slightly—makes them appear straight to the human eye, Ronan maintains.

Moreover, the creators of the Parthenon sidestepped just about every possible optical illusion by designing the building without a single straight line or right angle.

“Do you trust your eye? Or do you trust the numbers?” Ronan asks rhetorically. “This is the age-old question.”

But compensating for the quirks of human vision isn’t the only constraint in architecture. Practitioners already face enough challenges without adding a strictly proportioned rectangle to the mix, Ronan notes.

The size of the lot and the height of the building have a lot to do with the shape of the rectangles in the design, he says. Other impediments include building codes, the limits of technology and manufacturing, and conventional thinking that’s tethered to the familiar.

But just because the golden rectangle holds no special power in art and architecture doesn’t mean creative types don’t use it. 

Notable rectangles?

One of the most creative people who ever lived, Leonardo da Vinci, may have employed the golden rectangle extensively, according to some observers.

The very definition of a Renaissance man, da Vinci worked at the genius level as a painter, engineer, scientist, sculptor and architect. One of his many projects was illustrating a book by Franciscan friar and mathematician Luca Paioli on using the golden ratio in architecture. So, da Vinci was certainly aware of that possibility, Devlin says.

Some claim da Vinci used the golden rectangle in his paintings, including the Mona Lisa and The Last Supper. Others remain unconvinced by the rectangles drawn over photos of the paintings. 

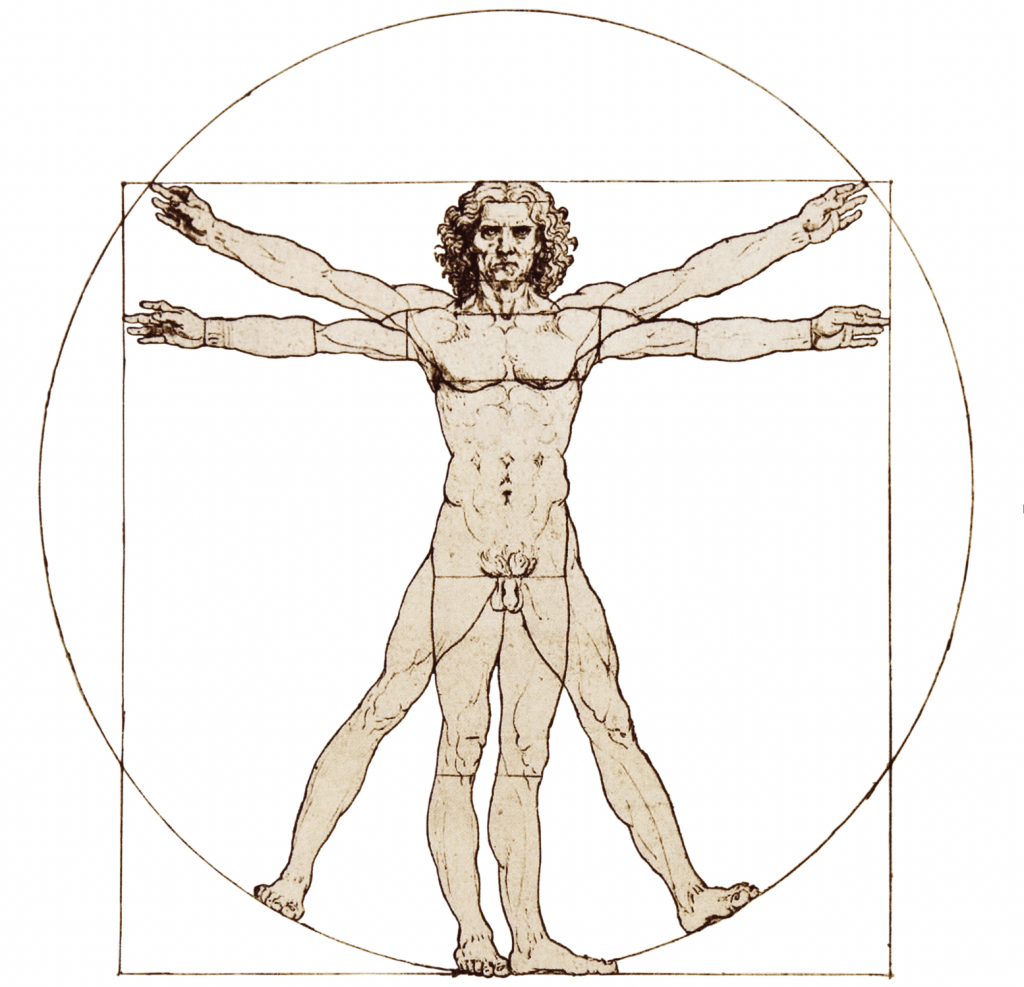
Then there was Vitruvian Man, a drawing da Vinci created to capture the ideal dimensions of the human body. Many have believed that bodily measurements, like height compared to the distance from the naval to the ground, conform to the ratio. It’s also been surmised that the most beautiful human faces adhere closely to spacing dictated by the ratio. Experiments show neither supposition holds true.

Not so golden

Overall, skepticism rules among the experts who spoke with Luckbox about the value of the golden ratio and golden rectangle in art and design.

“Renaissance architects were known for starting with those proportions because they thought there were quasi-magical qualities—if you hit the numbers that was a recipe for good design,” Illinois Tech’s Ronan says of the golden rectangle. “There are very few architects practicing that way in modern times.”

Cornell University’s Strogatz puts his thoughts on the golden ratio and rectangle this way: “In math, the golden ratio is a very real thing and has very wonderful properties. In botany and physics, the golden ratio is real. It just gets increasingly implausible as people try to stretch it to those other domains. That’s mostly mythology and culture.”

For Stanford’s Devlin, there’s nothing wrong with using the golden ratio in architecture as Le Corbusier so often did, but it just doesn’t work for art. “If you build artistic creations using the Fibonacci sequence, they look terrible,” he maintains. “There’s just not enough subtlety. For art, it really doesn’t work.”